NeurIPS 2025
Adversarial optimization algorithms that explicitly search for flaws in agents' policies have been successfully applied to finding robust and diverse policies in multi-agent settings. However, the success of adversarial optimization has been largely limited to zero-sum settings because its naive application in cooperative settings leads to a critical failure mode: agents are irrationally incentivized to self-sabotage, blocking the completion of tasks and halting further learning. To address this, we introduce Rationality-preserving Policy Optimization (RPO), a formalism for adversarial optimization that avoids self-sabotage by ensuring agents remain rational—that is, their policies are optimal with respect to some possible partner policy. To solve RPO, we develop Rational Policy Gradient (RPG), which trains agents to maximize their own reward in a modified version of the original game in which we use opponent shaping techniques to optimize the adversarial objective. RPG enables us to extend a variety of existing adversarial optimization algorithms that, no longer subject to the limitations of self-sabotage, can find adversarial examples, improve robustness and adaptability, and learn diverse policies. We empirically validate that our approach achieves strong performance in several popular cooperative and general-sum environments.
The interactive cross-play grids above show test-time robustness across different partners in the form of cross-play grids. Each row and column represents a single seed trained by either self-play (SP) with low or high entropy regularization, adversarial diversity (AD), or adversarial diversity - RPG (AD-RPG) (ours). The color of each square in the cross-play grid represents the average reward of the policies from the two associated seeds played against one another. AD-RPG consistently generalizes better across different partners. Click on any square in the grid to see a sampled rollout of the pair of policies.
In order to reap the benefits of adversarial optimization without incurring self-sabotaging behavior, we establish a new paradigm for adversarial optimization called Rationality-preserving Policy Optimization (RPO). We formalize RPO as an adversarial optimization problem that requires the policy to be optimal with respect to at least one policy that other agent(s) might play. This can be thought of as enforcing the agent to be rational: i.e., the agent must be utility-maximizing for some choice of teammates. RPO formalizes the rationality constraint as the following optimization problem:
$$ \begin{aligned} \max_{\pi_i} \ &O_i(\pi_1, \dots,\pi_m) \\ \text{subject to} \ &\exists \pi_{-i}' \text{ s.t. } \pi_i \in \text{BR}(\pi_{-i}'). \end{aligned} $$The rationality constraint imposed by RPO is difficult to directly integrate into a single optimization objective. To solve RPO, we introduce a novel approach called rational policy gradient (RPG), which provides a gradient-based method for ensuring rational learning while optimizing an adversarial objective. RPG introduces a new set of agents called manipulators, one for each of the agents in the original optimization problem (which we call base agents). In RPG, the base agents only train to maximize their own reward in a copy of the game (called its manipulator environment) with their teammates replaced by their manipulator counterparts -- this ensures that the base agents are solely learning to be rational. Each manipulator uses opponent-shaping to manipulate the base agents' learning and guide them towards policies that optimize the adversarial objective (e.g., achieving low reward with one another in the original base environment). The manipulators are discarded after training and the trained base agents give the solution to the RPO-version of the adversarial objective -- whether that be related to robustness, diversity, or some other objective. RPG allows us to use adversarial optimization in cooperative settings to find adversarial examples, robustify behavior, and discover diverse policies:

Figure 1: Rational policy gradient (RPG) allows finding rational adversarial examples, robustifying behavior, and discovering diverse policies.
Our main algorithm for training robust agents using RPG is called Adversarial Diversity - Rational Policy Gradient (AD-RPG), an RPG version of the adversarial diversity algorithm. AD-RPG trains robust agents by training a population of agents to simultaneously maximize their score with a partner while finding strategies that other agents in the population perform poorly against, ultimately improving the robustness of the entire population. We compare AD-RPG against classical adversarial diversity (AD) as well as self-play (SP) with both low (0.01) and high (0.05) entropy coefficients. Figure 2 shows the average in-population cross-play reward for each algorithm: the average of the cross-play scores from within the population of five seeds of each individual algorithm. AD-RPG performs better than all baselines across the Overcooked environments and comparably or stronger in Hanabi.
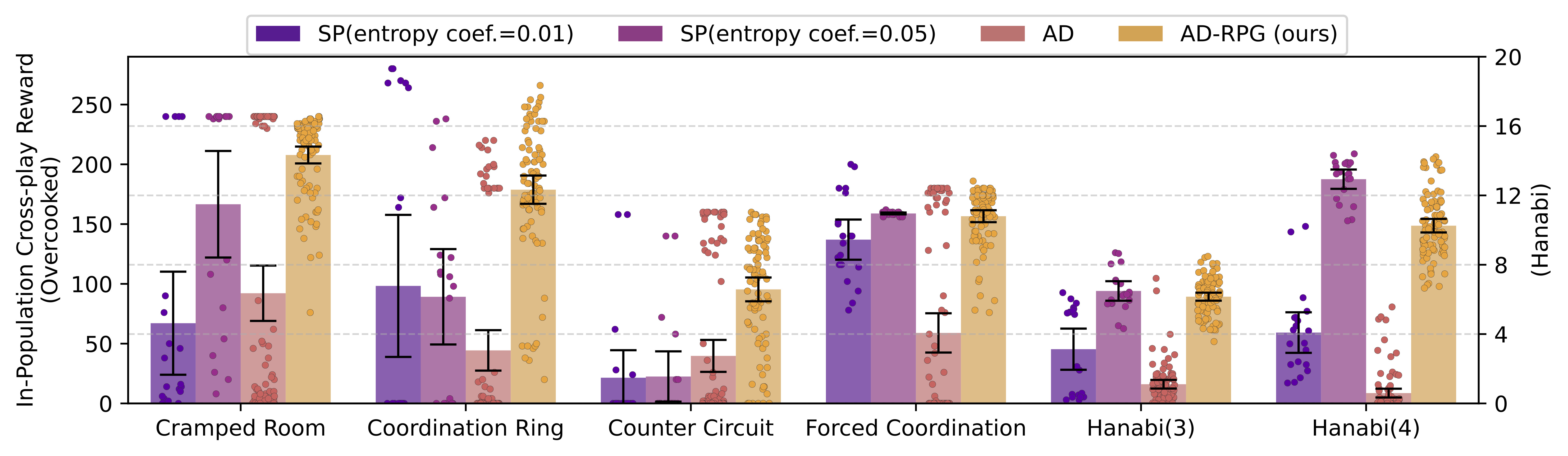
Figure 2: In-population cross-play rewards for different algorithms across environments. Points represent pairs of seeds, bar charts represent means, and error bars represent 95% confidence intervals.
RPG can also be used to create rational adversarial attacks that avoid self-sabotage. We tested the ability of AP-RPG to discover weaknesses in policies in the Cramped Room Overcooked layout. First, we trained a policy using self-play (SP) (visualized in Figure 2), then we used both AP and AP-RPG to search for a adversarial attacks. Visualized in Figure 3, AP (red agent) finds an irrational policy that sabotages the game by blocking the plate dispenser, a policy that achieves zero reward, but doesn't reveal any meaningful weaknesses in the SP policy (blue agent). Visualized in Figure 4, AP-RPG (red agent) is able to find a rational policy that achieves a reward of zero against the SP policy that identifies a meaningful weaknesses. Instead of simply sabotaging the game like AP, AP-RPG discovers that the victim (blue agent) assumes that the agents will move around each other clockwise. The manipulator in AP-RPG incentivizes the adversary (red agent) to instead move in a counterclockwise fashion, a perfectly rational strategy, though it happens to be incompatible with the victim.
Figure 2: A policy trained in self-play that learns to move clockwise around its partner.
Figure 3: An ordinary adversarial example (red agent) acts irrationally, simply blocking the plate dispenser and preventing progress.
Figure 4: A rational adversarial example (red agent) found by AD-RPG learns that the victim (blue) can't adapt to counterclockwise movement.
To explore the effectiveness of AT-RPG, PAIRED-RPG, AP-RPG, and PAIRED-A-RPG, we use a modified version of the STORM environment. Table 1 shows the performance of various fixed victims against different types of adversarial attacks. The "Victim" and "Training" columns indicate the algorithm used to train the victim and the reward achieved during training, respectively. The "AP", "PAIRED-A-RPG", and "AP-RPG" columns show the performance against these RPG adversarial attacks.
| Adversarial Attack Type | ||||
|---|---|---|---|---|
| Victim | Training | AP | PAIRED-A-RPG | AP-RPG |
| PAIRED | 0.13 | 0.0 | 0.50 | 0.42 |
| PAIRED-RPG | 0.93 | 0.0 | 0.84 | 0.85 |
| AT | 0.0 | 0.0 | 0.0 | 0.0 |
| AT-RPG | 0.65 | 0.0 | 0.72 | 0.88 |
| AD | 0.00 | 0.0 | 0.00 | 0.00 |
| AD-RPG | 0.98 | 0.0 | 0.25 | 0.96 |
| Self-play | 0.98 | 0.0 | 0.16 | 0.96 |
Table 1: The average reward that policies trained by various algorithms ("Victim" column) achieve against different adversarial attack types. The "Train" column shows the reward achieved during training and the following columns show the reward against different adversarial attack types. The AP attack trivially achieves zero reward because it self-sabotages.
As expected, every victim achieves zero reward against the AP attack since the adversary simply learns to self-sabotage the game by collecting no coins. Likewise, the non-RPG variations of algorithms (AT, PAIRED, AD) fail during training due to self-sabotage. PAIRED-A-RPG and AP-RPG are both able to find weaknesses in fixed policies and neither is susceptible to sabotage, PAIRED-RPG and AT-RPG training lead to more robust policies, indicated by high scores against both PAIRED-A-RPG and AP-RPG attacks.
@article{lauffer2025rpg,
title={Robust and Diverse Multi-Agent Learning via Rational Policy Gradient},
author={Lauffer, Niklas and Shah, Ameesh and Carroll, Micah and Seshia, Sanjit and Russell, Stuart and Dennis, Michael},
journal={Advances in Neural Information Processing Systems},
year={2025}
}